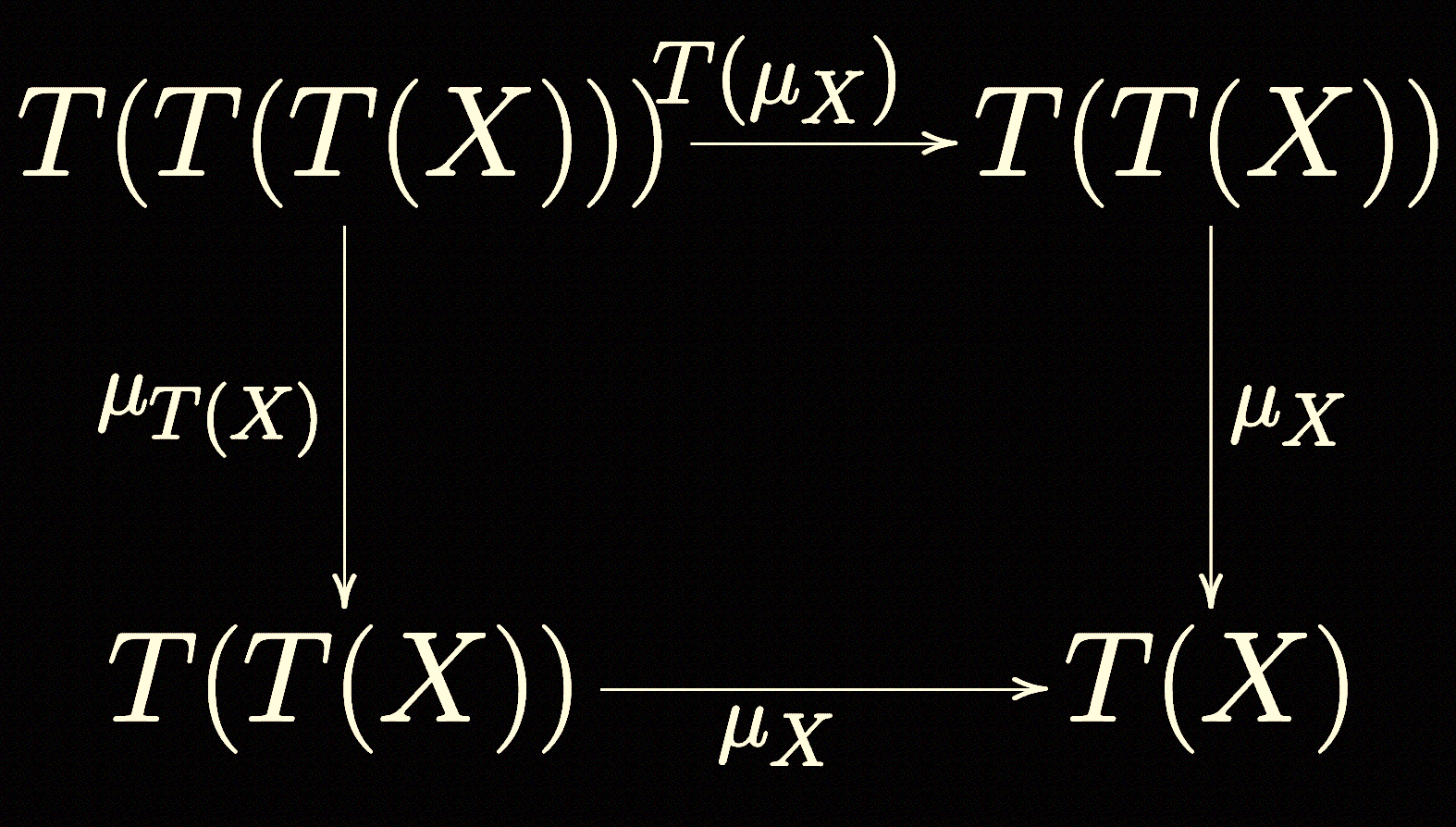Jon's Dev Blog
Jon's Dev Blog

Scala and Category Theory 1

February 17, 2021

I'm interested in the more category-theoretic aspects of functional programming. To this end, I have been working towards an elevator pitch on category theory for Scala devs (or alternatively, an elevator pitch on Scala for mathematicians). This is part 1.

What is Scala

Scala is a purely object oriented JVM language that supports functional programming.

What is Functional Programming

Functional programming (FP) is a programming theory of design in which programs are constructed by composing pure functions, that is, functions with well defined inputs and outputs and no side effects (i.e., mathematical functions). It is to be contrasted with imperative programming, in which case programs are interpreted as sequences of instructions fed to a machine.

Some aspects of functional programming that make it desirable:

  • Objects are stateless.
  • Functions are treated as "first-class citizens," i.e., they are treated as values of their own, with function type (more on that below).
  • Substitution model debugging is transparent and easy.

Theoretical Underpinnings

FP design is related to (or could be considered an example of) lambda calculus, which was defined by Alonzo Church in the 1930s to study computations with functions. Imperative programming, on the other hand, can be thought of as a design language more closely related to the concept of a Turing Machine.

So if you're wondering if they are truly equivalent (i.e., can any IP program be refactored as FP and vice versa), that is essentially the content of the Church-Turing Thesis.

An Example

From FP in Scala, let's look at an example to see how the two approaches differ. Suppose we want to write code for a cafe payment system. In an IP paradigm, we might write the payment system like so:

class Cafe {
  class Coffee {
    val price: Double
  }

  class CreditCard {
    var balance: Double

    def charge(amt: Double): Unit = {
      this.balance += amt
    }
  }

  def buyCoffee(cc: CreditCard): Coffee = {
    val cup: Coffee = new Coffee()

    cc.charge(cup.price) // Side-effect

    return cup
  }
}

// Elsewhere...

var cups: List[Coffee] = List()
for (i <- 0 until numCoffees) {
  cups :+= buyCoffee(cc)
}

// Get balance.
val balance = cc.balance

As you can see, the buyCoffee method calls the charge method of CreditCard, which changes the state of cc, and hence is not a pure (mathematical) function.

This is also harder to test and debug, since any unit tests would need to mock up a fake payment processing object (which would involve defining interfaces to abstract the essential traits, and introduce a lot of additional complexity).

A purely functional alternative to the above example is as follows.

class Cafe {
  class Coffee {
    val price: Double
  }

  class CreditCard {}

  case class Charge(cc: CreditCard, price: Double) {
    def combine(other: Charge): Charge = {
      if (this.cc != other.cc) throw new Exception("Mismatched credit cards.")
      else return Charge(this.cc, this.price + other.price)
    }
  }

  def buyCoffee(cc: CreditCard): (Coffee, Charge) = {
    val cup: Coffee = new Coffee()

    return (cup, Charge(cc, cup.price))
  }
}

// Elsewhere...

val purchases: List[(Coffee, Charge)] = (1 until numCharges).map(buyCoffee).toList

val (coffees, charges) = purchases.unzip

val finalCharge = charges.reduce((c1, c2) => c1.combine(c2))
val balance = finalCharge.price

The advantage of this approach is the referential transparency of the function buyCoffee, which makes it much easier to test and debug.

Types and Polymorphism

So FP is all about functions, and these functions are mathematical in nature. Another important concept here are types, which are conceptually the same as in Java or other non-functional languages (although Scala types are more structured, being a purely object-oriented language - more on that later).

A type is an attribute of an expression (e.g, the output of a function or a variable) in a computer program which allows a compiler to know what operations can be applied to it. For instance, an expression could be of type Int, String, Double, etc. Depending on the langugae, the user may also combine types or define new ones.

Function type

Functions that transform one type to another have their own type. In Scala, this is denoted using the "rocket symbol," =>. So for example, the expressions def f(x: A): B = ??? and val f: A => B = ??? are equivalent (with some caveats).

Polymorphism

In Scala, you can define functions to be polymorphic, which means they are parametrized by type. For example,

def map[A, B](f: A => B, things: List[A]): List[B] = {/* stuff */}

defines a function map, which transforms lists by applying a function f to them.

Algebra of Types

In scala, the set of all native types forms a category, where the objects are types and the morphisms are functions. In fact, this category is a distributive category. That is, a category with products and coproducts which satisfy the following conditions:

  • Both product and coproduct are associative.

  • Both product and coproduct have unit elements.

  • Product distributes over coproduct, i.e., there is a natural isomorphism

    A×(B⊔C)≃(A×B)⊔(A×C).A\times(B\sqcup C) \simeq (A\times B)\sqcup (A\times C).

The importance of thinking categorically is the change in perspective, i.e., rather than thinking about individual values, you think about whole types at once and understand them through their relationships with other types.

This is often phrased in terms of universal properties (ways of defining constructs, e.g., products, of types through relationships with constituents and other types).

Types in Scala

Category of Scala types:

  • Void - initial object. No values of type Void (it is an empty set).
  • Unit - terminal object. Think of it as a one element set containing the unique element ().
  • Products (A, B) of types A and B. These are tuples (cartesian product of sets).
  • Coproduct (direct sum / disjoint union). In Scala, this is Either[A, B], whose elements are Left(a) and Right(b).

Some other important types in scala are:

  • Option[A] - Whose elements are Some(a) or None. This is useful for FP error-handling
  • List[A] - Whose elements are Nil (empty list) or (a, as): (A, List[A]).

The bimonoidal properties in the Scala category take the form:

  • (A, (B, C)) = ((A, B), C)
  • (Unit, A) = A = (A, Unit)
  • Either[A, Either[B, C]] = Either[Either[A, B], C]
  • Either[Void, A] = A = Either[A, Void]
  • (A, Either[B, C]) = Either[(A, B), (A, C)]

You can construct other types using some basic building blocks as well. For instance,

  • Bool = Either[Unit, Unit]
  • Option[A] = Either[Unit, A] (i.e., Plus-one)
  • Nat = Either[Unit, Either[Unit, Either[Unit, ....]]]
  • List[A] = Either[Unit, (A, List[A])] (recursive)

Functors and Natural Transformations

Functors in Scala

Functors are mappings of categories (from one to another, or within a fixed category) that map objects to objects and morphisms to morphisms. In our case, functors are endomorphisms of the type tree, so types to types and functions to functions.

For example, List is a functor in the scala category. For any type A, we have a type List[A], and for any function f: A => B, we have the (implicitly defined) function _.map(f): List[A] => List[B]. In more formal syntax:

// This weird parametrization means it takes a parametrized type as a parameter.
trait Functor[F[_]] {
  def fmap[A, B](f: A => B): F[A] => F[B]
}

object ListFunctor extends Functor[List] {
  def fmap[A, B](f: A => B): List[A] => List[B] = (v: List[A]) =>
    v match {
      case Nil          => Nil
      case head :: tail => f(head) :: fmap(f)(tail)
    }
}

Functors which reverse arrows are called contravariant (the usual kind are called covariant). Scala supports covariance and contravariance in its functors as well! This is denoted by prepending a type parameter with a - for contravariance and a + for covariance. For example:

// Functions from A to B are covariant w.r.t. B
type CovariantHom[+B] = A => B
// Functions from B to A are contravariant w.r.t. B
type ContravariantHom[-B] = B => A

trait ContravariantFunctor[F[-_]] {
  def fmap[X, Y](f: X => Y): F[Y] => F[X]
}

object HomFunctor extends Functor[CovariantHom] {
  def fmap[X, Y](f: X => Y): CovariantHom[X] => CovariantHom[Y] =
    (g: A => X) => f.compose(g) // fg: A => Y
}

object ContravariantHomFunctor
    extends ContravariantFunctor[ContravariantHom] {
  def fmap[X, Y](f: X => Y): ContravariantHom[Y] => ContravariantHom[X] =
    (g: Y => A) => g.compose(f) // gf: X => A
}

Natural Transformations

If functors are the morphisms in the category of categories, then Natural Transformations are morphisms in the category of functors. So for every object A, we have a function eta[A]: F[A] => G[A]. There is a commutativity condition as well, so for any function f: A => B, it should be true that eta[B].compose(F.fmap(f)) = G.fmap(f).compose(eta[A]).

trait NaturalTransformation[F[_], G[_]] {
  def etaMapObs[X]: F[X] => G[X]
}

object HeadOption extends NaturalTransformation[List, Option] {
  def etaMapObs[X]: List[X] => Option[X] = (l: List[X]) =>
    // Pattern matching is like switch-case, but has nice qualities.
    l match {
      case Nil       => None
      case head :: _ => Some(head) // Scala way of saying (head, anything)
    }
}
Profile picture

Written by Jon Lamar: Machine learning engineer, former aspiring mathematician, cyclist, family person.