Snake Genetic Model

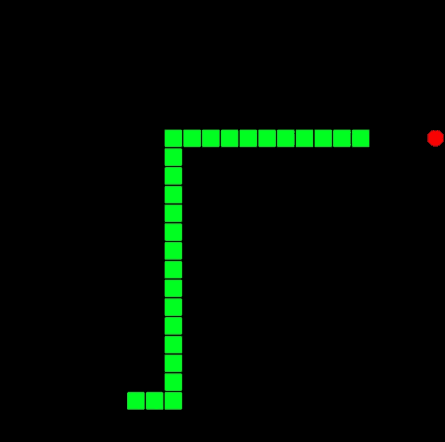
Overview

I wanted to build a neural network to play snake. My original idea was to use reinforcement learning, but I found a genetic solution and it seemed pretty simple to recreate.

Credit where it's due

I am basically porting this awesome repo to python in order to understand how the solution works.

My Final Product

Code here.

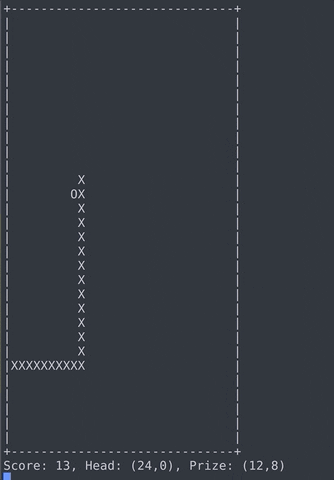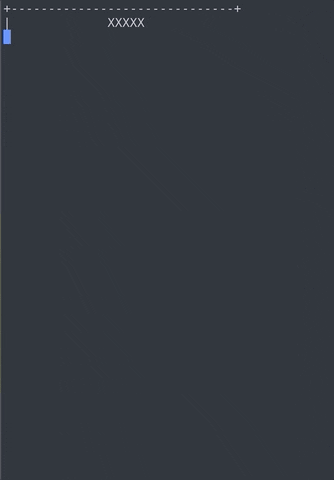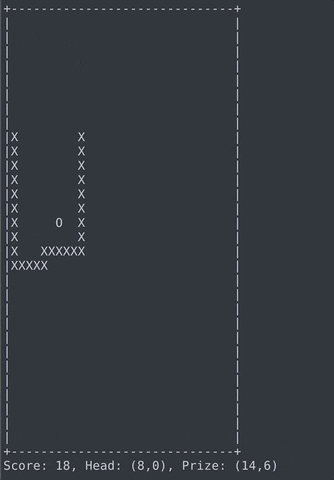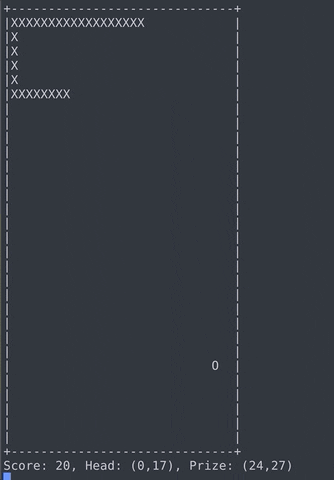
Goals

1. To get a neural network performing decently on a task.
2. Refresh my memory of how to use tesorflow and keras. (I've used them before, but never had much success with any of my projects.)
3. Enforce some python best practices I haven't been as rigorous about in the past. These include writing unit tests and following standard project structure.

Genetic algorithm

This model uses a genetic algorithm. That means that rather than optimizing weights by training on lots of examples, I am simply randomly initializing a bunch of players and letting them play. Their fitness is based on a scoring function, which considers both the overall performace and the length of the game played. I take the top performers and "breed" them to make the next generation of players. This process is repeated until the fitness stabilizes.

Performance metric

When a player plays, the game state iterates a variable (call it duration) each time the snake moves (i.e., for each time the game state advances by one frame). Each time the snake catches a prize, the game state iterates the score (call it score). The fitness metric function for the game is tunable by the user (located in the InitConfig class), but what I have settled on is of the form

fitness = np.log(1 + A*duration) + B*score

Breeding

Each generation, the program spawns generation_size players. Of those, it takes the top number_to_breed performers based on the above metric, and breed pairs at random with replacement to form generation_size more players for the next generation. To breed a pair of top performers, it chooses some of the weights from one and some from the other. I also apply Gaussian noise to introduce some randomness to the child. The variance of this noise can be thought of as a mutation rate, and is configurable by the user.

Remark

The repo I'm borrowing from did this in a nonrandom fashion, by performing a "crossover" operation for producing the weights in the child for each layer. In this operation, an index is selected uniformly at random, all child weights lexicographically before that index are drawn from the left parent layer, while all others are drawn from the right parent layer. I tried also selecting values uniformly, but the former algorithm yielded better breeding.

The neural network

The architecture of the network is somewhat customizable by setting the parameters num_hidden_layers and hidden_layer_size in the InitConfig class. I use a standard fully connected network with an input layer of size 24, num_hidden_layers hidden layers each of size hidden_layer_size, and an output of dimension 4. Unfortunately, these cannot be changed without starting over. The inputs encode that the snake is looking in 8 directions (four cardinal and four diagonal). In each direction, it is looking for a prize, distance to a wall, and itself. The outputs encode which direction to move.