Metrics for Evaluating Recommender Systems

May 01, 2024

Adding some notes I took on recommender systems while working at Vizio. This is not proprietary knowledge, and is just a summary of some metrics introduced in a paper linked below.

Notation

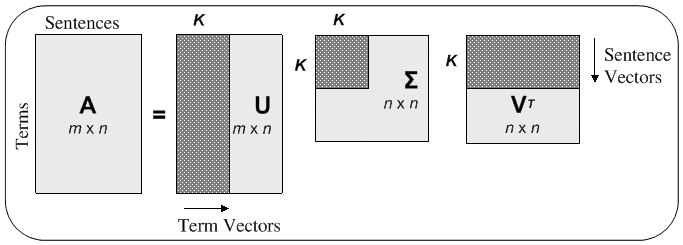
We are primarily concerned with implicit feedback recommender systems, and those based on matrix factorization methods (ALS, SVD, etc.). In this family of algorithms, the goal is to factor the feedback matrix $R$ into a product of two rectangular matrices of latent factor representations.

Notation for Explicit Feedback Models

More precisely, Let $m$ be the number of users, let $n$ be the number of movies, and let $k$ be the number of latent factors. Let $R\in\mathbb{R}^{m\times n}$ be the feedback matrix, so that $R = (r_{u,i})$ , where $r_{u,i}$ is some feedback signal about the preference of user $u$ for title $i$ . Let $X\in\mathbb{R}^{k\times n}$ be the matrix of genre weights for the movies, and let $\Theta\in\mathbb{R}^{m\times k}$ be the matrix of genre preferences for the users. Then

R \simeq \Theta\cdot X.

Implicit Feedback

The above is the traditional setting of explicit feedback, where $r_{u,i}$ is something like a rating (thumbs up/down, or a 0 to 5 score). In this setting, the feedback matrix represents preference. In the implicit feedback setting, $r_{u,i}$ is usually based on consumption (number of views, for example). In this case, the feedback matrix represents confidence about titles. As such, there is no notion of negative feedback. One way to deal with this, outlined in the Hu, Koren, Volinsky paper, is the use of a preference signal

p_{u,i} = \mathbb{1}_{r_{u,i} > C}

and a confidence signal

c_{u,i} = 1 + \alpha\cdot\log(1 + r_{u,i} / \epsilon).

The confidence signal is used as a term weighting in the alternating least squares formula, while the feedback matrix is replaced with the preference matrix $P = (p_{u,i})$ .

Metrics

Recall (haha) that precision is the ratio of true positives to reported positives. In the language of recommender systems, this is the proportion of recommendations that are actually relevant. Similarly, recall is the proportion of relevant titles that are recommended.

We define relevance in terms of $P$ : if $p_{u,i} = 1$ , title $i$ is relevant for user $u$ , otherwise it is not. We can define recommendations a couple of different ways. If we form predictions $\widehat{p_{u,i}} = \theta^{(u)}\cdot x^{(i)}$ , and rank titles based on the (floating point) values of these predictions, then recommendations could either be the top $K$ titles based on this ranking, or the top $K$ , excluding those below a predefined relevance threshold. Either way, we have a well-defined notion for true and false positives and negatives.

MAP@ $K$

For any user and any positive integer $i$ , define

TP_{\text{seen}}(i)_u = \left\{\begin{matrix} \#\{\text{true positives in the top $i$ recommendations}\} & : & \text{$i$th recommendation is TP} \\ 0 & : & \text{otherwise} \end{matrix}\right.

Then we can define average precision at $K$ for any user as

\text{AP@$K$}_u = \frac{1}{TP_{\text{seen}}(K)_u}\cdot\sum_{i=1}^K\frac{TP_{\text{seen}}(i)_u}{i}.

We define mean average precision at $K$ to be the mean of AP@ $K$ over all users.

Why MAR@ $K$ Is Not Very Useful

We can adapt the above formulas for a recall-oriented metric instead, by defining AR@ $K$ to be the average recall seen at $i$ , as $i$ ranges from 1 to $K$ . In this case, the formula becomes

\text{AR@K}_u = \frac{1}{TP_{\text{seen}}(K)_u}\sum_{i=1}^K\frac{TP_{\text{seen}}(i)_u}{\#P},

where $\#P$ is the total number of positives (i.e., the total number of relevant titles).

The first issue is that because recall depends more on the titles not recommended than on the titles recommended (i.e., it is dominated by the denominator if there are a lot of titles watched), the above equation is dominated by the final term in the sum. Thus, there is not really a lot of information gained over using just averaging recall at $K$ over all users:

The second issue with this metric is that the scale is no longer intuitive. To see this, consider the best possible case: where all $K$ recommended titles are relevant. Then we would have

\text{AR@K} = \frac{1}{K}\sum_{i=1}^K\frac{i}{\#P} = \frac{K+1}{2\cdot\#P},

which is not equal to 1 in general, and will be a very small number most of the time.

Expected Percentile Ranking

The Hu et al paper used expected percentile ranking as one of their main metrics for comparing recommender systems. It is easy enough to define. Let $\text{rank}(u,i)$ denote the percentile rank of title $i$ for user $u$ , i.e., the rank of the recommendation (in terms of relevance) divided by the number of titles recommended. Then

\mathbb{E}(\text{rank}) = \frac{\sum_{u,i}r_{u,i}^t\cdot \text{rank}(u,i)}{\sum_{u,i}r_{u,i}^t},

where $r^t$ denotes relevance calculated during the test period.

Thus, expected percentile rank can be thought of as a weighted average of percentile rank by consumption, so the range is $[0,1]$ and lower is better.

Why this tells a different story than precision

$\mathbb{E}(\text{rank})$ is a normalized weighted sum of rank by relevance. Thus, it is higher if we are omitting heavily viewed titles from our recommendations, even if precision is high. From this point of view, expected ranking can be thought of as a recall-oriented metric.

Empirical CDF of percentile ranking

The authors also look at the distribution of percentile rankings by plotting the CDF and comparing models. This seems fairly qualitative, unless we do AUC or something.