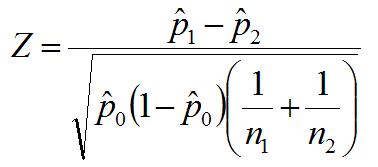A Statistical Test for Difference of Two Rates

Adding notes I took while trying to understand how to AB test an intervention on churn rate.

Setup

The Scenario

Suppose we are a subscription service, and we want to A/B test a new campaign to increase usage among low activity viewers. Suppose also we do not have good information on expected return rate from month to month (e.g, because we have not collected data previously to establish a baseline population return rate). In this scenario, we will need to use separate test and control groups, and test the difference between test and control group's return rates after the intervention. To make things concrete, let's say we measure the return rate at the end of every month, and the intervention is a push notification or something that fires sometime during the month of study. Moreover, and these devices have been chosen because they are at a relatively low level of activity.

Notation

• Let the subscript $i\in\{t, c\}$ denote that a quantity is calculated for the test or control group, respectively.
• Let $P_i$ denote return rate.
• Let $Q_i = 1-P_i$.
• Let $N_i$ denote the observed number of returners in group $i$.
• Let $n$ be the sample size for the test and control groups (i.e., there are $2n$ total participants).
• Let $\alpha$ and $\beta$ be the usual definitions of type I and II error, respectively.
• For any real number $\gamma$, let $z_{1-\gamma}$ be the usual standard normal cutoff quantile.

Objective

Note that $N_i \simeq Binom(n, P_i)$. Assuming $n$ is large, then $Binom(n, P_i) \sim N(N_i, n\cdot P_i\cdot Q_i)$. Since we are dealing with a lot of customers and there is little risk in using large samples, we may assume $n$ is large and the differences are negligible. Therefore, we can use a suitable $z$ statistic to test the difference $N_t - N_c$, which is approximately distributed as $N(n(P_t - P_c), n(P_tQ_t - P_cQ_c))$.

Since we hope to reduce return with this campaign, let's assume the null hypothesis is that $P_t \leq P_c$, and the alternative hypothesis is $P_t>P_c$.

Calculating the $z$-Statistic

Let

Assuming the null hypothesis, we reject if $z > -z_{\alpha}$. Under the null hypothesis, $P_t - P_c \geq 0$. In fact, we can assume $P_t = P_c$ under the null, so that our rejection region is as small as possible. In other words, define

and define the rejection region as

Deciding Sample Size

Power is defined to be

But this expression is true if and only if the right hand side is $z_{1-\beta}$. Therefore, we have